Combinação com repetição

Para introduzirmos o conceito de combinação com repetição, é importante relembrar a definição formal de combinação simples.
Considere n objetos diferentes. Se tratarmos da contagem do número de maneiras de escolher k dentre esses n objetos sem considerarmos a ordem, então criamos uma combinação destes elementos sem repetição. A fórmula para obter esta combinação é dada por:

Cn,k=n!k!(n−k)!

Por exemplo, imagine o seguinte cenário: Estamos organizando um campeonato de xadrez com 12 participantes. De quantas maneiras possíveis podemos criar as duplas para disputar a primeira partida? Este problema pode ser solucionado calculando a combinação de 12 jogadores organizados de 2 em 2. Que nos traz:

C12,2=12!2!(12−2)!=12!2!⋅10!=12⋅11⋅10!2!⋅10!=12⋅112=66

Temos então 66 formas diferentes de organizar as duplas a partir dos 12 primeiros participantes. Há uma outra notação para a operação de combinação, ou coeficiente binomial, que é dada por:

Cn,k=(nk)=n!k!(n−k)!

Agora, quando a ordem dos elementos pode ser repetida, então tratamos de uma combinação com repetição. A fórmula será dada, neste caso, por:

Cn+k−1,k=(n+k−1k)=(n+k−1)!k!(n+k−1−k)!

Ou seja:

Cn+k−1,k=(n+k−1)!k!(n−1)!

Vejamos agora um exemplo aplicado:
Exemplo 1) Supondo que você queira comprar um sorvete com 4 bolas em uma sorveteria que possui 3 sabores disponíveis: chocolate, baunilha e morango. De quantos modos diferentes você pode fazer esta compra?
Note que nesta combinação, é possível repetir a ordem de dois ou mais sabores, assim tratando de uma combinação com repetição. Se temos 3 sabores disponíveis e queremos uma combinação para 4 bolas, pela fórmula obtemos:

Cn+k−1,k=(n+k−1)!k!(n−1)!

C3+4−1,4=(3+4−1)!4!(3−1)!

C6,4=6!4!⋅2!=6⋅5⋅4!4!⋅2!=6⋅52=302=15

Logo, temos 15 combinações possíveis para esta compra!
ENEM 2017) Um brinquedo infantil caminhão-cegonha é formado por uma carreta e dez carrinhos nela transportados, conforme a figura.

No setor de produção da empresa que fabrica esse brinquedo, é feita a pintura de todos os carrinhos para que o aspecto do brinquedo fique mais atraente. São utilizadas as cores: amarelo, branco, laranja e verde, e cada carrinho é pintado apenas com uma cor. O caminhão-cegonha deve haver pelo menos um carrinho de cada uma das quatro cores disponíveis. Mudança de posição dos carrinhos no caminhão-cegonha não gera um novo modelo do brinquedo. Com base nessas informações, quantos são os modelos distintos do brinquedo que essa empresa poderá produzir?
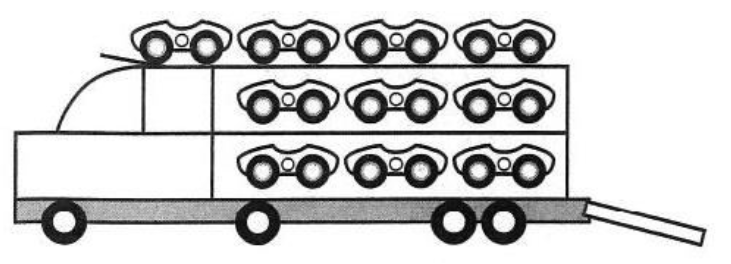
Note as palavras em negrito no texto. Pela interpretação da questão percebe-se que ela se trata de uma combinação com repetição. Então, se temos 4 cores disponíveis e 10 carrinhos a ser colocados no brinquedo a questão pode ser solucionada da seguinte maneira:
Pelo exercício, teremos pelo menos um carrinho de cada cor. Então podemos supor que existe uma quantidade (amarelo), (branco), (laranja) e (verde) e mais um de cada, no mínimo. Então podemos dizer:

• Carrinho amarelo: a+1
• Carrinho branco: b+1
• Carrinho laranja: L+1
• Carrinho verde: v+1

Somando então estas quantidades, sabemos que o total deve ser igual a 10 carrinhos, o que nos leva a:

a+1+b+1+L+1+v+1=10

Isolando as variáveis temos que:

a+b+L+v=10−4

a+b+L+v=6

Ora, perceba que agora temos um cenário onde já sabemos que ao mínimo teremos um carrinho de cada cor, que já ocupa 4 posições no caminhão-cegonha restando apenas 6 posições. Então é necessário pensar que devemos organizar agora 4 carrinhos em 6 posições considerando a repetição. O que nos leva a formula:

Cn+k−1,k=(n+k−1)!k!(n−1)!

C4+6−1,6=(4+6−1)!6!(4−1)!

C9,6=9!6!⋅3!=84

Referências Bibliográficas
MEYER, Paul L. Probabilidade: Aplicações à Estatística. São Paulo: Editora Livros Técnico Científicos, 1975.
Prova – ENEM 2017, Questão 143 – Prova Azul

Origem: https://www.infoescola.com/matematica/combinacao-com-repeticao/