CONJUNTOS NUMÉRICOS

A noção de conjunto numérico é bastante simples e fundamental na Matemática. A partir dos conceitos sobre conjuntos podemos expressar todos os conceitos matemáticos.

Um conjunto nada mais é do que uma coleção qualquer de objetos. Por exemplo:

1. conjunto das estações do ano: E = {Primavera, Verão, Outono, Inverno}
2. conjunto dos números primos: B = {2, 3, 5, 7, 11, 13, ...}

Cada item dentro de um conjunto é um elemento desse conjunto.
A ideia dos conjuntos numéricos segue uma ordem de acordo com a história da Matemática. Ou seja, à medida que a matemática avançou, foi necessário a criação de novos conceitos e, com isso, foram surgindo vários conjuntos de números.

Conjunto dos números naturais (N)

N={0,1,2,3,4,5,6,...}

O número zero é o primeiro elemento desse conjunto. O sucessor de cada número nesse conjunto é igual à soma dele mesmo com uma unidade, ou seja, o sucessor de 3 será 4 pois 3 + 1 = 4.
Para representar o conjunto dos números naturais não-nulos (ou seja, diferentes de zero), deve-se colocar um * ao lado do símbolo:

N∗={1,2,3,4,5,6,...}

Conjunto dos números inteiros (Z)

Em determinada época da história, se fez necessário a criação de números que representassem “perdas”, ou “dívidas”. Surgiram, assim, os números negativos. Esses números negativos, junto com os números naturais, formam o conjunto dos números inteiros:

Z={...,−3,−2,−1,0,1,2,3,...}

Nesse conjunto, para cada número há o seu oposto, ou seu simétrico, por exemplo, 3 e -3 são opostos ou simétricos.
Veja que todo número natural é inteiro, mas nem todo número inteiro é natural. Dizemos que o conjunto dos números naturais está contido no conjunto dos números inteiros.

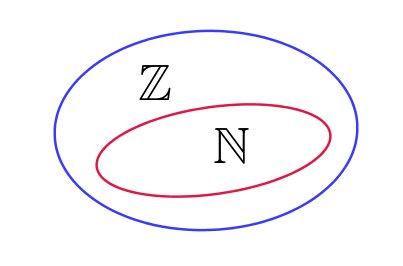
Conjunto dos números racionais (Q)

Com a necessidade de descrever partes de algo inteiro, surgiram as frações. Quando adicionamos as frações aos números inteiros, obtemos os números racionais. São exemplos números racionais:

Q={−1,−25,43,5,...}

Formalmente, um número racional é todo aquele que pode ser escrito na forma de uma fração. Assim,

Q={x/x=ab,a∈Z,b∈Z,b≠0}

Observe que todo número inteiro é racional, mas nem todo número racional é inteiro. Por exemplo, -1 é inteiro e é racional, mas 43 é racional e não é inteiro. Assim, o conjunto dos números inteiros está contido no conjunto dos números racionais: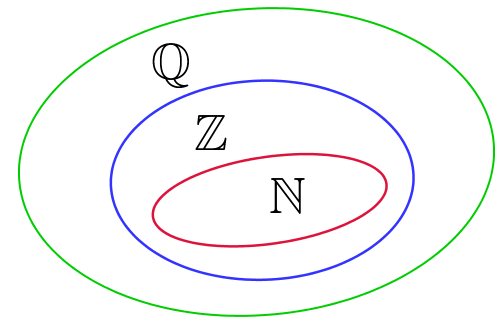

Conjunto dos números irracionais (IR)

O conjunto dos números irracionais é composto por todos os números que não são possíveis de se descrever como uma fração. É o caso das raízes não exatas, como 2–√, 3–√, 5–√, e do número π, do logaritmo neperiano, o número de ouro ϕ (fi), por exemplo.
Este conjunto não está contido em nenhum dos outros três, ou seja, nenhum número irracional é racional, inteiro ou natural e nenhum número natural, inteiro ou racional é irracional.

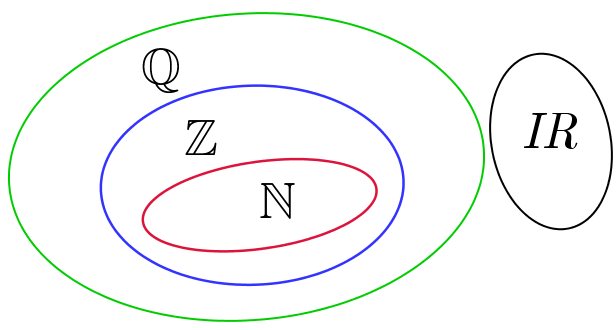
Conjunto dos números reais (R)

Da reunião do conjunto dos números racionais com os números irracionais obtemos o conjunto dos números reais. Podemos dizer que o conjunto dos números reais é formado por todos os números que podem ser localizados em uma reta numérica.
Assim, todo número que é irracional é real, assim como os naturais, inteiros e racionais.

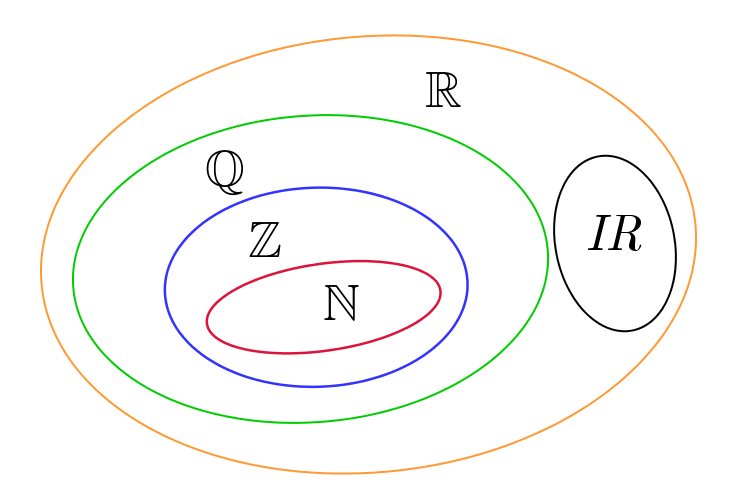
Existem ainda conjuntos maiores, que englobam todos vistos até aqui. Um exemplo é o conjunto dos números complexos. São números que possuem uma parte real e uma arte imaginária, chamada de “i”. São números da forma a+bi, onde a é a parte real e b é a parte imaginária.
Referência:
DANTE, Luiz Roberto. Matemática: contexto & aplicações. 2. ed. Vol 1. São Paulo: Ática, 2013.